The first part of this series can be found here: Algorithmic Trading- a novelty still inaccessible to the masses.
Prerequisites:
My work throughout my tenure as Software Development intern at Symphony Fintech was majorly focussed on developing a feature which can allow the user to get stock-specific recommendations for the ideal set of parameters for any given indicator-based signals, either pre-defined or user-designed, based on the performance of the strategy over the historical data of the concerned stock(Backtesting).
For any given indicator, all possible combinations of parameter values would mean dealing with a vast search space; hence brute-forcing through the procedure would imply a sluggish performance. The introduction of every parameter would result in another dimension being added to the search space causing the time required to run the program to increase exponentially with each such addition. Since the execution time is of significant importance, the option of training Neural Network-based models for the job doesn’t seem to fit with the problem requirements. Plus, in such a system where the definition of a gradient isn’t clearly defined, derivative-based methods prove out to be problematic. Genetic Algorithms provide an efficient and adaptive approach towards such a modifiable problem statement with a vast search space and discrete cost functions.
We’ll go over the concept of Genetic Algorithm below. In order to give you as much information about the workings of this feature, we’ll go through the implementation of the same in C#. In case you aren’t interested in the concept of GA and how this feature works internally, feel free to skip the following two sections and jump to the Deployment section, where I’ve explained how the user can get access to this feature and use it.
Genetic Algorithms are a subclass of Evolutionary algorithms widely used for optimization purposes. These are inspired by the biological phenomenon of evolution. These algorithms operate by mimicking the principles of reproduction and natural selection to constitute search and optimization procedures. Therefore, it becomes essential to know a little about Darwin’s Theory of Evolution. We won’t cover the biological correspondence of GA in deep since that is outside the scope of this blog, but we will go through the major concepts required for the understanding of this feature of our library.

Keeping these points in mind, we can now discuss how we arrive at the solution. While moving through the search space, there are two kinds of searches that we focus on
As the names suggest, the former is a more reserved searching procedure mostly confined to the surroundings of the current best solution. In the context of GA, this is achieved using the Crossover operator. The latter is a more comprehensive searching procedure spanning the complete domain. This is handled by the mutation operator. Before explaining the operators involved and how they come into use, we need to know about what a Fitness Function is.
The function to be optimized in the problem statement is called the Objective Function(OF). The Fitness function is derived using the objective function. It is used to evaluate each individual formed during the procedure and forms the basis for Natural Selection. If the problem statement involves maximizing the OF, the fitness function is taken to be same as the objective function i.e.
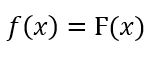
On the other hand, if the PS involves the minimization of the OF, we convert it into a maximization problem by considering the reciprocal of the original OF (add 1 to the denominator to account for the function being zero-valued at some points) and then take the modified OF as the fitness function:
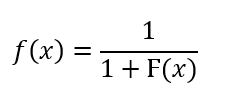
In our case, we have a maximization type problem; hence the objective function can be taken to be the fitness function. Due to this, we might use the two terms interchangeably. Although I’ll try me best not to ;).
This is based on the principle of Natural Selection “A Fitter individual has a higher survival duration and is more suited for the environment.” This operator is used to identify individuals from the current lot, who are more likely to contribute to the development of the final solution (fittest individual). The individuals are ranked based on the fitness values (obtained from the fitness function) of each of them. Then the top few individuals are chosen to be used for further offspring formation and to keep the evolution going.
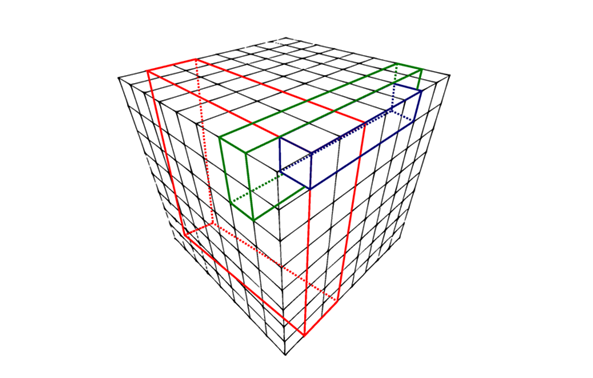
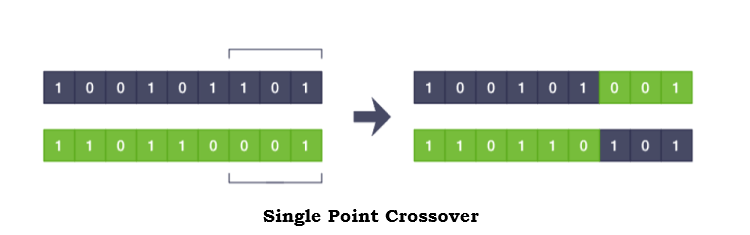
The crossover operator forms the basis of the complete GA algorithm which facilitates the formation of the offsprings from parents’ genetic information. It generates the chromosomes of the child using the parental chromosomes by simply swapping certain parts from both of them. If the chromosomes are broken into two parts (breakpoint can be anywhere) and crossed over, it is called a single-point crossover, which is depicted in the adjoined diagram. There are various such methods with the chromosomes being broken up into more number of parts. In the XFinChart library, we use a single point crossover.
The mutation operator deals with providing a distinctiveness to the next generation by making some changes in the offsprings generated through the Crossover. It takes care of the concept of ‘variations’ mentioned in Darwin’s Theory. This ensures the offsprings’ properties don’t just remain bounded by the characteristics their parents possessed. There are multiple approaches while implementing the mutation operator, namely, Random Resetting, Swap, Scramble, etc. In the XFinChart library, we make use of the Random Resetting mutation, which involves changing a random gene of the chromosome.

Crossover and Mutation operators help implement the walk through the search space in quest of the best-suited solution. It is carried out in a manner to improve the quality (fitness values) of the solutions.
As we have covered most of the topics required for proceeding further, we can follow through the application of GA in our problem statement. We’ll start by formulating the PS.
Note: You may encounter the term ‘signal’ on numerous instances through the blog. By Signal, I mean the implementation of the trading strategy involving an indicator.
Problem Statement: Given an Indicator based Market Strategy, optimize the parametrical values for the Signal to maximize the profits obtained as a result of Backtesting the strategy on historical data.
(Later, we’ll discuss involving other statistics terms of the trades into the objective function alongside the Profit.)
The population in the context of GA involves the set of variables that need tweaking in order to maximize the Fitness Function.
![]()
For example, in the moving average crossover strategy, the parameters are the time-periods of the long-term and short-term moving averages. Since I’ve chosen a strategy involving only two parameters, the grid would be two dimensional. With every addition, an extra dimension will be added to our search space.
Each individual of the population involves a set of values for the parameters; in GA terminology, this representation is referred to as a chromosome and the individual components as genes. Visualize it as an array of values, each corresponding to one of the parameters of the indicator. This representation allows us to convert a point from an n-dimensional space to a 1-dimensional structure. Every such array points to a particular point in the n-dimensional search space. We first need to define a randomly chosen population and supply it to the algorithm to seed the process, which is depicted in the following snippet. The reader need not worry about the last line of the snippet. It is simply assigning a random allowable value to the parameter.
private void InitialPopulation(){
Random r1 = new Random();
for (int i = 0; i < _population_size; i++){
for (int j = 0; j < _num_parameters; j++)
_population[i, j] = Math.Round((r1.NextDouble() * (_upper_limits[j] - _lower_limits[j]) + _lower_limits[j]),
(int)_decimal_count[j], MidpointRounding.ToEven);
}
}
The adjoined code snippet shows how the algorithm computes the fitness value of an individual. Methods RunBackTesting and FitnessValue are used to calculate the overall Backtesing statistics and the final Fitness Value, respectively. You might not understand the exact workings of the function, but I’ll try to give you a gist of what it actually intends on executing.
private void ComputePopulationFitness(){
for(int i = 0; i < _population_size; i++){
for(int j = 0; j < _num_parameters; j++)
_optimizer_details[j].PropertyCurrentValue = _population[i, j];
Dictionary<string, double> statistics = _tsOptimizationInfo.RunBackTesting(_optimizer_details);
_generation_fitness[i] = _tsOptimizationInfo.FitnessValue(statistics);
}
}
The OptimizationDetail class is an inherent class of the XFinChart library that stores the information regarding a particular parameter, which helps define the limits of the search space to be used in the optimization procedure. The TSOptimizationInfo is a class that stores information such as the list of parameters of the indicator and various other information needed to define the setup of the complete GA algorithm. The objects of these classes are used in the ComputePopulationFitness() function.
OptimizationDetail[] _optimizer_details; TSOptimizationInfo _tsOptimizationInfo;
The first step (effectively) of the procedure involves ranking all the chromosomes based on their fitness values (obtained by computing the fitness function using the parametrical values enclosed in the genes). A fixed number of the top fittest chromosomes are identified, thus forming the Mating Pool. This number is captured by the Retention Ratio that the user sets up (don’t worry, that too is explained later on). It decides what percentage of the new generation should be from the Mating Pool. The rest comes from the Reproduced (Crossover + Mutation) offspring. The individuals of the Mating Pool will act as parents for the next generation.
private void MatingPool(){
int i, j;
for (i = 0; i < _retention_count; i++){
//use temp array to push fitter chromosomes into the compacted search space
//CAUTION--do not put this type declaration outside the loop. We need a completely new object every time,
//to be passed to the List containing the parameter sets to the compacted search space
double[] temp = new double[_num_parameters];
var maxValue = _generation_fitness.Max();
int maxIndex = _generation_fitness.ToList().IndexOf(maxValue);
for(j = 0; j < _num_parameters; j++){
temp[j] = _population[maxIndex, j];
_parents[i, j] = _population[maxIndex, j];
}
_compact_space.Add(temp);
_generation_fitness[maxIndex] = Double.MinValue;
}
}
The next step involves forming offspring using the chromosomes of the mating pool. Thus, the Crossover operator comes into play, which creates offsprings using the genetic encoding of the parental chromosomes. The individuals of the Mating Pool act as parents in this step. A single point crossover (involving two equal sections of the chromosome) has been implemented in the library.
private void CrossoverOperator(){
int parent1_idx, parent2_idx, crossover_point = _num_parameters / 2;
for (int k = 0; k < _population_size - _retention_count; k++){
parent1_idx = k % _parents.GetLength(0);
parent2_idx = (k + 1) % _parents.GetLength(0);
for (int p = 0; p < _num_parameters; p++){
if (p < crossover_point) _crossover_set[k, p] = _parents[parent1_idx, p];
else _crossover_set[k, p] = _parents[parent2_idx, p];
}
}
}
If you have a bit of an experience analyzing optimization processes or data analysis, you definitely will be well aware of the concepts of Global maxima/minima and Local maxima/minima. But for others, the former is the definitive point where you need an algorithm to achieve while the latter is just some point elsewhere in the search space, which might give the false alarm of reaching the desired point. So, to avoid converging to a local-maxima, the next step becomes increasingly essential. The implementation of the mutation operator ensures that the algorithm continues to explore uncharted territories for the possibilities of better solution sets. The procedure for Random Resetting Mutation instructs that we take a set of the chromosomes produced earlier using Crossover and randomly change some genes from it.
In the adjoined snippet, the value of a random gene, of a random chromosome, is being reassigned a random value in accordance with the permissible range of the parameter. The number of chromosomes to be mutated depends on another customizable variable known as the Mutation Ratio, which decides the percentage of the offspring (generated through Crossover), which is to be Mutated.
private void MutationOperator(){
int random_index, random_chromosome;
Random r1 = new Random();
double random_value;
Array.Copy(_crossover_set, _mutation_set, _crossover_set.Length);
for (int i = 0; i < _mutation_count; i++){
//Choose a parameter and a chromosome both radomly and change it
random_index = r1.Next(0, _num_parameters);
random_chromosome = r1.Next(0, _mutation_set.GetLength(0));
//Get a random value(in accordance with the increment value) in the associated range
random_value = Math.Round((r1.NextDouble() * (_upper_limits[random_index] - _lower_limits[random_index])
+ _lower_limits[random_index]), (int)_decimal_count[random_index], MidpointRounding.ToEven);
_mutation_set[random_chromosome, random_index] = _lower_limits[random_index] + ((random_value
+ _mutation_set[random_chromosome, random_index]) % (_upper_limits[random_index]- _lower_limits[random_index]));
}
}
We now append our resultant population sets coming from Mating Pool and Mutation. This marks the end of a single generation of the process, thus providing us with a new population to begin with.
private void EvolvePopulation(){
for (int j = 0; j < _population_size; j++){
if (j < _retention_count){
for (int k = 0; k < _num_parameters; k++)
_population[j, k] = _parents[j, k];
}else{
for (int k = 0; k < _num_parameters; k++)
_population[j, k] = _mutation_set[j - _retention_count, k];
}
}
}
The same processes are then applied over the newly formed population over and over again, thus creating new generations every time. During this complete process in each generation, the algorithm tries to find the most optimized chromosome using the operators. After a certain number of generations, the fitness value of the best fit chromosome becomes constant, indicating that the algorithm has achieved the maxima.
For the successful deployment, we need to set up a set of variables properly to ensure we get the desired results. These are to be set from the point where you intend to access the Genetic Algorithm class.
The data file containing the data should be loaded by specifying the complete path in the filename variable. If the file is located in the same folder as the program the user is currently operating in; the exact file name can be used independently.
string fileName = @"C:\Users\Desktop\XFinChartJune2020\TSTestApp\bin\Debug\ACC.txt";
Next, we need to load the data from the file in a data structure which can easily be used for further operations. The TimeDataSeries class provides the ideal data structure for this job. It also presents various options to the user based on their requirements, such as Bar Compression type, Bar type, etc. The second line of the snippet loads the data (which is in the form of OHLCVO columns) into an object of the above class.
TimeDataSeries timeDataseries = new TimeDataSeries(BarCompression.MinuteBar, 60, BarType.CandleStick); timeDataseries.LoadDataFromFile(fileName, OHLCFileFormat.Symbol_Date_Time_O_H_L_C_V_O, DateFormat.Year_Month_Day);
The user needs to configure their formed strategies. There exist the options for customizing any such strategy configuration parameter in the StrategyConfigData class. Some of them are depicted below. Another such parameter is ‘OrderExecutionAt’ through which the user can set whether the trade has to be initiated at the close of the current bar or the open of the next bar. There are numerous such options for the user to configure their strategies. You can set any of these parameters simply through the object of this class.
StrategyConfigData strategyConfigData = new StrategyConfigData(); strategyConfigData.InitialCapital = 100000; strategyConfigData.MinTickSize = .05; strategyConfigData.Pyramiding = PyramidingType.Allow; strategyConfigData.MaxPyramidingPosition = 4;
Next, the user needs to set up the instrument details wherein the user provides information about the concerned stock. It consists of a unique ID which will be specific to the security, setting the exchange in which the security trades, tick size of the data and the expiry.
Instrument instrument = new Instrument(111, "NSECM", "ACC", 20, 1, DateTime.MaxValue);
Now, the user needs to register the signal to be used with the Signal Registration Manager using the code below. Also, the signal name needs to be specified separately. In the code, we’re using a dual EMA crossover signal with the name of TestSignal.
SignalRegistrationManager.Instance.RegisterSignal(typeof(TestSignal)); string signalName = "TestSignal";
If you’ve jumped right into the Deployment section, you need to know that the OptimizationDetail class is an inherent class of the XFinChart library that stores the information regarding a particular parameter, which helps define the limits of the search space to be used in the optimization procedure. The TSOptimizationInfo is a class that stores information such as the list of all parameters of the indicator and various other information needed to define the setup of the complete GA algorithm. The next snippet depicts how it is required to be set up. While storing the parameter information in an OpmizationDetail object, the order of the data should be Parameter Name, the Lower limit of its permissible range, Upper limit of its permissible range, Increment Value. The Increment value stores the precision of the values that are allowed. For Ex: If the parameter can take up integer values only, then it should be set to 1 and if the range for a parameter is [5,100] and the values can be 5, 5.1, 5.2, ….. then the Increment value would be set to 0.1 and so on. So the increment value parameter expects values of 1/0.1/0.01/… and so on, depending upon the requirement.
TSOptimizationInfo tsOptimizationInfo = new TSOptimizationInfo(instrument, timeDataseries, strategyConfigData, signalName);
// StartValue, EndValue, IncrementValue
OptimizationDetail emaFastLengthOptimizationDetail = new OptimizationDetail("FastLengthPeriod", 10, 50, 1);
OptimizationDetail emaSlowLengthOptimizationDetail = new OptimizationDetail("SlowLengthPeriod", 50, 100, 1);
Then each of these objects storing the parameter detail is added to the TSOptimizationInfo as optimization variables meaning that the GA program would operate to get an optimal set of these parameters. Note that if not added as an optimization variable to the object of the TSOptimizationInfo class, that parameter won’t be considered for the process.
tsOptimizationInfo.AddOptimizationVaraibles(emaFastLengthOptimizationDetail); tsOptimizationInfo.AddOptimizationVaraibles(emaSlowLengthOptimizationDetail);
The statistical variables that the user intends to inculcate in the OF are specified in the following manner. For setting up a range based term in the Objective Function, i.e., if the user requires some statistic to be in a particular range, then the upper and lower limits have to be supplied alongside, as seen in the second line of the snippet. In the case of Minimization/Maximization terms in the OF, only the name has to be specified.
tsOptimizationInfo.AddMaximizeObjFuncTraget("NetProfit");
tsOptimizationInfo.AddRangeObjFuncTraget("PercentProfitable", 0.3, 0.35);
tsOptimizationInfo.AddMinimizeObjFuncTraget("GrossLoss");
Now, the final configurations that the user has to set up are the Core GA parameters, after which we just need to run the algorithm, which is very straightforward and can clearly be understood by the code below. In case of doubts regarding the definitions of these parameters, refer to the theory mentioned in the previous sections.
XTS.TS.Core.Optimizer.GASimpleOptimizer gaSimpleOptimizer = new XTS.TS.Core.Optimizer.GASimpleOptimizer(tsOptimizationInfo); gaSimpleOptimizer.SetGenerationCount=5; gaSimpleOptimizer.SetMutationRatio = (float)0.25; gaSimpleOptimizer.SetPopulationSize = 50; gaSimpleOptimizer.SetRetentionRatio = (float)0.3; gaSimpleOptimizer.Run();
Now, after the program is done running, the program will give out information regarding the final results that the algorithm has achieved, such as, the values of the terms included in the OF and the recommended set of parametrical values for the signal. Now the XFinChart library also allows you to get access to a smaller and more focussed search space which might help you in your further analysis. To get the Condensed search space provide the commands as depicted in the next snippet.
List<double[]> search_space= new List<double[]>(); search_space = gaSimpleOptimizer.GetCompactSpace;
In most applications of GA that we come across, the desired result is the point where we finally have the fitness function give the maximum (reminder: even the minimization type PS is converted into this form) value. But in our context, one finds that during the course of its run, the algorithm encounters multiple such chromosomes with different genes that possess the fitness equal to the maximum fitness value or which are close to it. While developing this feature, our only intention wasn’t just to provide the analyst a point in the search space, which gives us this value, but we were also interested in finding out all such points encountered which have good fitness values. What this does is it provides the analyst with a more focussed search space with a lot of noise removed, thus allowing the analyst to perform additional analysis on a personalized level over this condensed search space. The extent of this downscaling can be huge, especially in cases when the analysts run complex algorithms or use indicators with multiple parameters causing the search space to be housing a million points, thereby causing the process to be heavy, cumbersome, and time-taking for the system. This feature will enable the processes to run in a much shorter time, making them more efficient.
The first part of this series can be found here: Algorithmic Trading- a novelty still inaccessible to the masses.
To learn more about designing your indicators or using predefined templates from the XFinChart library, go through the following blog.
Thanks!